Advent of Code - Day 18

(heatmap slicing a 3-D piece of lava - all in SQL!)

Disclaimer

This article will contain spoilers both on how I solved 2022 Day 18's challenge "Boiling Boulders" using SQL, as well as general ideas on how to approach the problem. I recommend trying to solve it yourself first, using your favorite language.

AOC Day 18

Tech:

🐘 The ever important file_fdw

🐘 Using sequences as a crude numbering aid

🐘A recursive CTE to help expand our flat data into a 3-d table

🐘 The generate_series function and a ON CONFLICT DO NOTHING to populate "holes" in our table.

🐘 Functions written in plpgsql to solve the puzzle and draw some colorful output using Unicode and terminal escape sequences.

For Day 18, we have rescued the elephants, and now we must analyze a falling lava boulder, gather its total surface area, and determine if it will turn into obsidian. The input file looks like this:

2,2,2
1,2,2
3,2,2
2,1,2
2,3,2
2,2,1
2,2,3
2,2,4
2,2,6
1,2,5
3,2,5
2,1,5
2,3,5

The numbers represent coordinates of the blocks that make up the block of lava. Let’s create a table for this data:


CREATE UNLOGGED TABLE aoc_day18 (
    x smallint,
    y smallint,
    z smallint
);

INSERT INTO aoc_day18 (x, y, z) VALUES (2, 2, 2);
INSERT INTO aoc_day18 (x, y, z) VALUES (1, 2, 2);
INSERT INTO aoc_day18 (x, y, z) VALUES (3, 2, 2);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 1, 2);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 3, 2);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 2, 1);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 2, 3);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 2, 4);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 2, 6);
INSERT INTO aoc_day18 (x, y, z) VALUES (1, 2, 5);
INSERT INTO aoc_day18 (x, y, z) VALUES (3, 2, 5);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 1, 5);
INSERT INTO aoc_day18 (x, y, z) VALUES (2, 3, 5);

AOC 2022 Day 18 Part One

Our first task is to determine the total surface area of the lava boulder. In other words, for each of the cubes represented by rows in the file, how many are their six sides are adjacent to another block, and how many are free? This was simple to solve with a recursive CTE. We walk through each cube, and get a count of how many other cubes are next to it. In the case of this three-dimensional grid, another cube is adjacent if two of the three coordinates are the same, and the third one only differs by a single number. Once we have the number of blocked sides, we subtract that from the total sides across all cubes and have our surface area solution:


CREATE SEQUENCE aoc;

WITH recursive r AS (
SELECT 0::bigint AS id, 0 AS x, 0 AS y, 0 AS z, 0::bigint AS occ
UNION ALL
SELECT a.*,
(SELECT count(a.*) FROM aid a2 JOIN aid a ON
  (
    a.id <> a2.id AND
    (a.x=a2.x AND a.y=a2.y AND (a.z=a2.z+1 OR a.z=a2.z-1))
    OR
    (a.x=a2.x AND a.z=a2.z AND (a.y=a2.y+1 OR a.y=a2.y-1))
    OR
    (a.y=a2.y AND a.z=a2.z AND (a.x=a2.x+1 OR a.x=a2.x-1))
  )
  WHERE a.id = r.id+1
)
FROM aid a JOIN r on (a.id = r.id+1)
)
, aid AS (SELECT nextval('aoc') AS id, * FROM aoc_day18)
, occluded AS (SELECT sum(occ) AS occluded_sides FROM r)
, totalsides AS (SELECT 6*count(*) AS total_sides FROM aoc_day18)
SELECT *, total_sides - occluded_sides AS exposed_sides from occluded, totalsides;

This runs pretty fast for plain SQL: 1.1 seconds for the real data set (consisting of 2,192 cubes), and 2 milliseconds for the test data set shown above (consisting of 13 cubes).

AOC 2022 Day 18 Part Two

For part two there is, as they say in the baking competitions I watch, a "twist". The block of lava has some coordinates indicating where the rock is, but now we need to consider the air as well! If the inside of the lava contains air pockets that are unreachable from the outside, then any exposed rock surfaces forming that pocket get excluded from the surface calculation. Time to roll up our sleeves, throw away that recursive CTE, and put things into a proper SQL table. The solution will be to figure out which cubes of air are "leaky" and exposed to the outside, and which are internal only. In other words, we are going to be doing some iterating, keeping track of state, and modifying attributes of each of our blocks. SQL is actually pretty good at all that, via the UPDATE statement. First, we'll create a table to store our information. Besides the three coordinates given by the input (which we have called, X, Y, Z), we are going to track what type of block this is (rock or air), and whether it is leaky or not.


CREATE TABLE rocks AS SELECT *, 'rock'::TEXT AS type, NULL::bool AS leaky
  FROM aoc_day18;
CREATE UNIQUE INDEX rocky_unique ON rocks(x,y,z);

That unique index will come in handy as we can use it to power our ON CONFLICT DO NOTHING clause to fill our table with air blocks, but only in places where there is not already a rock block. We want to make sure the air surrounds the rock completely, so we go a little outside the min and max for each direction in our generate_series calls:


INSERT INTO rocks SELECT a,b,c,'air'::text
FROM
  generate_series( (select min(x)-1 from rocks), (select max(x)+1 from rocks)) a,
  generate_series( (select min(y)-1 from rocks), (select max(y)+1 from rocks)) b,
  generate_series( (select min(z)-1 from rocks), (select max(z)+1 from rocks)) c
ON CONFLICT DO NOTHING;

At this point, we have everything we need - any air block on the outer edge of the giant cube we created is, by definition, leaky. So we will write a function to walk through and propagate that leakiness to any other air blocks that it touches. The function:


CREATE or replace FUNCTION airwalk()
  returns void language plpgsql AS
$$
DECLARE
  lowx INT; lowy INT; lowz INT;
  bigx INT; bigy INT; bigz INT;
BEGIN
  SELECT INTO lowx, lowy, lowz, bigx, bigy, bigz
    min(x), min(y), min(z), max(x), max(y), max(z) FROM rocks;

  /* Every air block on the outside is by definition leaky */
  UPDATE rocks d SET leaky=true
    WHERE type='air'
    AND (x=lowx OR y=lowy OR z=lowz OR x=bigx OR y=bigy OR z=bigz);

  /* Always a good idea, as we are about to do some heavy querying */
  ANALYZE rocks;

  /* Iterate through and spread the leakiness as far as we can */
  LOOP

    /* Mark any air block touching a leaky air block as also leaky */
    UPDATE rocks r SET leaky=true
      WHERE type='air' AND leaky IS NULL
      AND EXISTS (SELECT 1 FROM rocks r2 WHERE leaky AND (
           (r2.y=r.y AND r2.z=r.z AND (r2.x=r.x+1 OR r2.x=r.x-1))
        OR (r2.x=r.x AND r2.z=r.z AND (r2.y=r.y+1 OR r2.y=r.y-1))
        OR (r2.x=r.x AND r2.y=r.y AND (r2.z=r.z+1 OR r2.z=r.z-1))
       ));

    /* Keep doing this until there is nothing left to update */
    IF NOT FOUND THEN EXIT; END IF;

  END LOOP;

  /* Count the total rock faces that are attached to a leaky air block */
  RAISE NOTICE 'Final count: %',
    count(*) FROM (
    SELECT 1 FROM rocks r1 WHERE type='rock'
      AND EXISTS (SELECT 1 FROM rocks r2 WHERE leaky 
                  AND r1.x=r2.x AND r1.y=r2.y AND r1.z = r2.z+1)
    UNION ALL SELECT 1 FROM rocks r1 WHERE type='rock'
      AND EXISTS (SELECT 1 FROM rocks r2 WHERE leaky
                  AND r1.x=r2.x AND r1.y=r2.y AND r1.z = r2.z-1)
    UNION ALL SELECT 1 FROM rocks r1 WHERE type='rock'
      AND EXISTS (SELECT 1 FROM rocks r2 WHERE leaky
                  AND r1.z=r2.z AND r1.y=r2.y AND r1.x = r2.x-1)
    UNION ALL SELECT 1 FROM rocks r1 WHERE type='rock'
      AND EXISTS (SELECT 1 FROM rocks r2 WHERE leaky
                  AND r1.z=r2.z AND r1.y=r2.y AND r1.x = r2.x+1)
    UNION ALL SELECT 1 FROM rocks r1 WHERE type='rock'
      AND EXISTS (SELECT 1 FROM rocks r2 WHERE leaky
                  AND r1.x=r2.x AND r1.z=r2.z AND r1.y = r2.y+1)
   UNION ALL SELECT 1 FROM rocks r1 WHERE type='rock'
     AND EXISTS (SELECT 1 FROM rocks r2 WHERE leaky
                 AND r1.x=r2.x AND r1.z=r2.z AND r1.y = r2.y-1)
   ) z;

END
$$;

Before running, we can speed it up a tiny bit by dropping that unique index, as it is not needed anymore. We will replace it with a partial index based on the fact that we often ask for rows that are leaky.


DROP INDEX rocky_unique;
CREATE INDEX bb on rocks(x,y,z) WHERE leaky;
SELECT airwalk();

This runs very fast. For the real data set, it takes 207 milliseconds. For the test data, it takes 7 milliseconds.

AOC 2022 Day 18 Bonus Round!

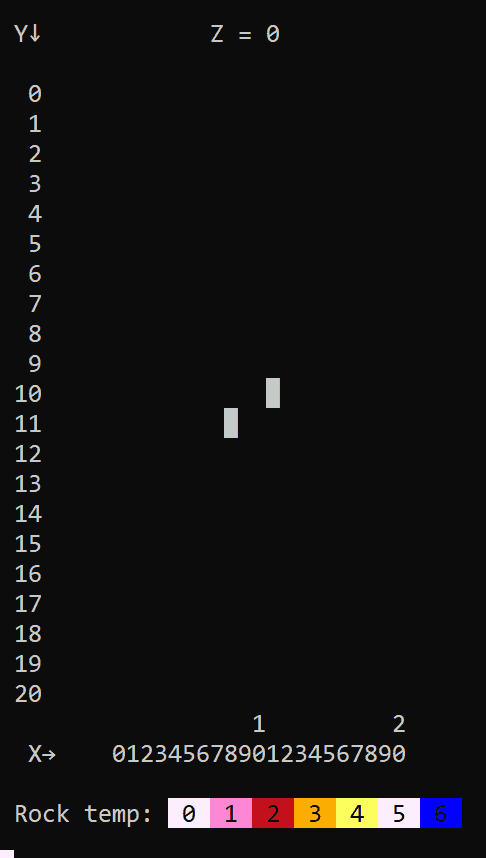
The puzzle is complete. But wait, you say, can we get a pretty graphic? Yes, we can! While this lava blob is a 3-D image, we can draw it by showing a slice at a time, similar to a CT scan. We could show only the rocks and air blocks, but let's make it more interesting by turning it into a heatmap as well. We know that surface area is important, so the amount of heat that each block receives is a function of how many of its faces get exposed. Let's add a new column to our table to track the number of exposed sides for each "rock" block:


ALTER TABLE rocks ADD sides INT;
UPDATE rocks SET sides = 0;

UPDATE rocks r1
  SET sides = (SELECT count(*) FROM rocks r2 WHERE r2.type='air' AND r2.leaky
    AND (
      (r2.x=r1.x AND r2.y=r1.y AND (r2.z=r1.z+1 OR r2.z=r1.z-1))
    OR (r2.z=r1.z AND r2.y=r1.y AND (r2.x=r1.x+1 OR r2.x=r1.x-1))
    OR (r2.x=r1.x AND r2.z=r1.z AND (r2.y=r1.y+1 OR r2.y=r1.y-1))
  ))
WHERE type = 'rock';

Now we have enough information for a function to draw the lava boulder, where the X and Y appear as on a graph, while the Z axis gets revealed over time as we slice our way through the boulder. We use Unicode symbols and ASCII colors to make things look pretty, and the trick of clearing then immediately redrawing the screen as a form of animation. We'll also label the axes and add a legend to explain our heat map. Finally, we'll scan the boulder in one direction, then reverse and scan the other way. Any air blocks that are NOT leaky, and thus completely enclosed by rocks, appear as small purple dots. If you look at the final result at the top of this post, you'll see that there is definitely a large air pocket in the middle of the lava boulder. Here's the function:


CREATE or replace FUNCTION drawit()
  returns void language plpgsql AS $$
DECLARE
  myrec RECORD; mytext TEXT = ''; oldy INT;
  mycolor TEXT; myclear TEXT = E'\033[0m';
  legend TEXT;
  xrow TEXT = format('%s1%s2%s  X%s    012345678901234567890',
    repeat(' ',18),repeat(' ',9),chr(10),U&'\2192'); /* Unicode 2192 "right arrow" */
  maxz INT = (SELECT max(z) FROM rocks WHERE type = 'rock');
  current_slice INT = 0;
  zoffset INT = +1;

  pinky    TEXT = E'\x1b[38;5;225m';  pinkybg    TEXT = E'\x1b[48;5;225m';
  lightred TEXT = E'\x1b[38;5;212m';  lightredbg TEXT = E'\x1b[48;5;212m';
  red      TEXT = E'\x1b[38;5;196m';  redbg      TEXT = E'\x1b[41m';
  orange   TEXT = E'\x1b[38;5;214m';  orangebg   TEXT = E'\x1b[48;5;214m';
  yellow   TEXT = E'\x1b[38;5;227m';  yellowbg   TEXT = E'\x1b[48;5;227m';
  white    TEXT = E'\x1b[38;5;231m';  whitebg    TEXT = E'\x1b[48;5;231m';
  blue     TEXT = E'\x1b[38;5;21m';   bluebg     TEXT = E'\x1b[48;5;21m';
  black    TEXT = E'\x1b[38;5;0m';    purplish   TEXT = E'\x1b[38;5;165m';

BEGIN

  /* As things heat up they go from red to orange to yellow to white to blue #science */
  legend = FORMAT(' Rock temp: %s%s 0 %s 1 %s 2 %s 3 %s 4 %s 5 %s 6 %s',
    black, pinkybg, lightredbg, redbg, orangebg, yellowbg, whitebg, bluebg, myclear);

  LOOP

   /* Set the header; 033c clears the screen; Unicode 2193 is "downwards arrow" */
   mytext = format('%s%s Y%s            Z = %s%s',
     E'\033c', chr(10), U&'\2193', current_slice, chr(10),chr(10));

   /* Reset our variable to detect if we are in a new row */
   oldy = -99;

   /* For the current Z slice, pull all interesting X and Y coordinates */
   FOR myrec IN SELECT * FROM rocks WHERE y>=0 AND z=current_slice ORDER BY y,x LOOP

     /* When Y has changed, start a new row */
     IF oldy <> myrec.y THEN
       oldy = myrec.y;
       mytext = mytext || format('%s %2s%s', chr(10), myrec.y, '    ');
     END IF;

     /* Set default colors for rocks and air */
     mycolor = CASE WHEN myrec.type='rock' THEN pinky ELSE purplish END;

     /* Number of exposed sides indicates its temperature */
     IF myrec.sides = 1 THEN mycolor = lightred; END IF;
     IF myrec.sides = 2 THEN mycolor = red;      END IF;
     IF myrec.sides = 3 THEN mycolor = orange;   END IF;
     IF myrec.sides = 4 THEN mycolor = yellow;   END IF;
     IF myrec.sides = 5 THEN mycolor = white;    END IF;
     IF myrec.sides = 6 THEN mycolor = blue;     END IF;

     /* Draw the item at this position, with coloring */
     mytext = mytext || format('%s%s%s',
       mycolor,
       (CASE WHEN myrec.type = 'air' THEN
         /* Unicode 00B7 is "middle dot" */
         CASE WHEN myrec.leaky THEN ' ' ELSE U&'\00B7' END
         /* Unicode 2588 is "full block" */
       ELSE U&'\2588' END),
       myclear);
   END LOOP;

   /* Output the entire current slice, then sleep a little to animate */
   RAISE NOTICE '% % %', mytext, chr(10)||xrow, chr(10)||chr(10)||legend;
   PERFORM pg_sleep(0.2);

   /* If we have sliced the entire thing, turn around and slice the other direction! */
   IF current_slice = maxz THEN perform pg_sleep(1); zoffset = -1; END IF;
   IF current_slice = 0 AND zoffset=-1 THEN perform pg_sleep(1); zoffset = +1; END IF;

   current_slice = current_slice + zoffset;

  END LOOP;
END;
$$;


SELECT drawit();

Voila!

Loading terminal...