Elevation Profiles and Flightlines with PostGIS
5 min readMore by this author
A community member on the postgis-users mailing list had a question recently:
I have a table of elevation points, and I would like to figure out an elevation profile for a flightline running through those points. How?
This question is a nice showcase of some of my favorite spatial tools with indexing, point to point distance queries on a sphere, and nearest neighbor queries. I thought it would make a great post. The original question author was nice enough to share his elevation data, so I can show you some pictures and an approach.
Elevation Points every 2KM
The data set is 1.5M elevation points in Europe, one point for every 2km. When plotted on a map you can see this is quite dense.
The table structure is simple.
Column | Type | Collation | Nullable | Default
-----------+------------------+-----------+----------+---------
latlng | geography | | |
lat | double precision | | |
lng | double precision | | |
elevation | real | | |
All we need is a spatial index on the latlng column to make our nearest neighbor searches fast.
CREATE INDEX elevation_latlng_x ON elevation USING GIST (latlng)
Flightlines
Flightlines are different from overland lines because they are not only "as the crow flies", but "as the crow flies over a sphere". Over longer distances, and at higher latitudes, the effect is more visible, but great circle routes are not quite the same as point-point routes.
For example, a straight line between London and Warsaw can be constructed like this:
SELECT ST_MakeLine(ST_MakePoint(-0.061,51.482), -- London
ST_MakePoint(21.252,52.150)) -- Warsaw
But a straight line (shortest path over a plane) is not what we want, we want a great circle (shortest path over a sphere). So, we flip the line into the geography type, which uses great circles to interpolate between vertices, and then ST_Segmentize the line, to add new vertices between the endpoints.
SELECT ST_Segmentize(geography(
ST_MakeLine(
ST_MakePoint(-0.061,51.482),
ST_MakePoint(21.252,52.150))
), 4000)
The red line is the great circle, the blue line is the original cartesian line.

Nearest to a Point
For the final query, we will construct a flight path between Madrid and Guadalajara, two cities close enough together that we can see the actual elevation points. We'll put a vertex every 4KM along that path, and find the closest elevation point to each vertex.
To find the closest point, we use the <-> "index ordered distance" operator. When placed in the ORDER BY clause of a query <-> not only calculates the distance between the left and right operands, it also returns the distances starting from the minimum possible distance.
So, the query for the nearest elevation point to Madrid (-3.6996,40.4009) is:
SELECT
e.elevation,
ST_AsText(e.latlng, 3) AS coords,
geography(ST_MakePoint(-3.6996,40.4009)) <-> e.latlng AS dist
FROM elevation e
ORDER BY dist
LIMIT 1
Which returns (in 2ms, because of the index assist):
elevation | coords | dist
-----------+----------------------+--------------------
650.8142 | POINT(-3.707 40.409) | 1045.4185642910293
Nearest to Flight Path
The index-assisted nearest neighbor operator <-> is an odd one, as it requires a literal value on one side of the operator. It cannot take in two variable arguments, so how do we join up our flight path, which will have more than one point, to the elevation grid?
The answer is to use a LATERAL JOIN to control the iteration and supply the flight path points, one at a time, to the nearest neighbor calculation.
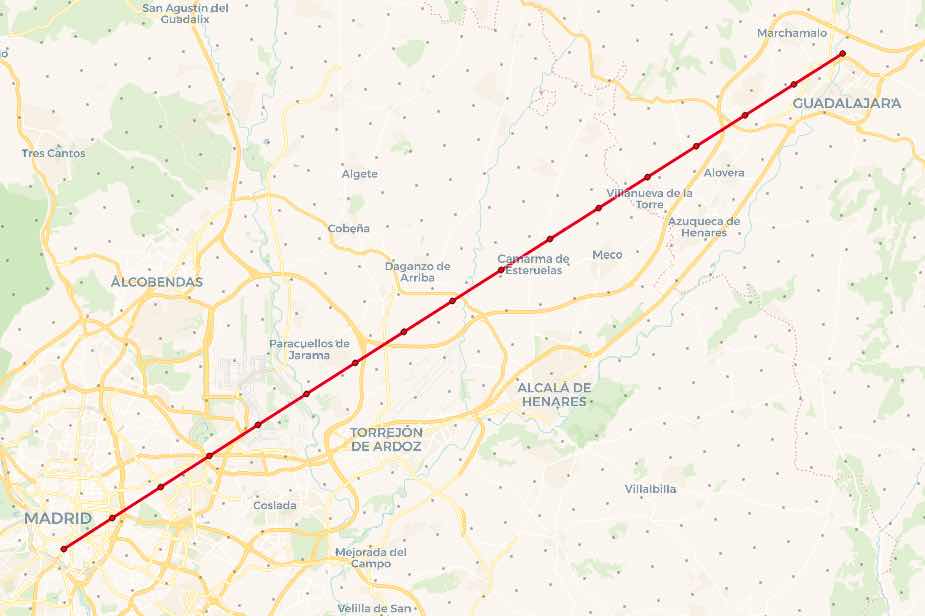
Taken in chunks, the query first builds the flight path.
WITH path AS (
SELECT ST_Segmentize(geography(
ST_MakeLine(
ST_MakePoint(-3.6996,40.4009), -- Madrid
ST_MakePoint(-3.1675,40.6582)) -- Guadalajara
), 4000) AS geog
)
Then it takes apart the path into one record for each vertex using ST_DumpPoints
points AS (
SELECT (ST_DumpPoints(geog::geometry)).geom FROM path
)
Finally, it does a lateral join to the elevation points, finding the nearest elevation for each path point.
SELECT
d.elevation,
round(d.dist) AS distance,
ST_AsText(d.latlng, 3) AS elevation_pt,
ST_AsText(points.geom, 3) AS path_pt
FROM points
CROSS JOIN LATERAL (
SELECT
e.elevation, e.latlng,
points.geom::geography <-> e.latlng AS dist
FROM elevation e
ORDER BY dist
LIMIT 1
) d
The final result take about 14ms to run, and finds an elevation for every point on the flightline.
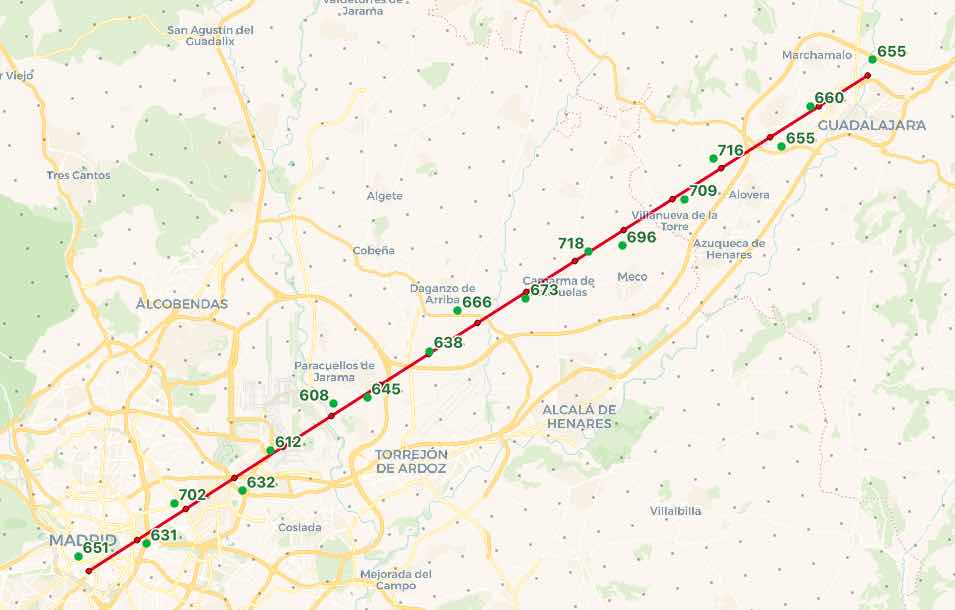
elevation | distance | elevation_pt | path_pt
-----------+----------+----------------------+----------------------
650.8142 | 1045 | POINT(-3.707 40.409) | POINT(-3.7 40.401)
630.8268 | 563 | POINT(-3.66 40.415) | POINT(-3.666 40.417)
701.6845 | 728 | POINT(-3.641 40.436) | POINT(-3.633 40.433)
632.26556 | 882 | POINT(-3.595 40.443) | POINT(-3.6 40.449)
611.845 | 733 | POINT(-3.575 40.464) | POINT(-3.567 40.465)
607.7102 | 701 | POINT(-3.533 40.488) | POINT(-3.534 40.482)
644.5825 | 1057 | POINT(-3.509 40.491) | POINT(-3.501 40.498)
637.69604 | 166 | POINT(-3.467 40.515) | POINT(-3.467 40.514)
666.1685 | 1335 | POINT(-3.447 40.536) | POINT(-3.434 40.53)
673.436 | 373 | POINT(-3.401 40.543) | POINT(-3.401 40.546)
717.8294 | 938 | POINT(-3.358 40.567) | POINT(-3.368 40.562)
696.11383 | 910 | POINT(-3.335 40.57) | POINT(-3.334 40.578)
709.38855 | 723 | POINT(-3.292 40.594) | POINT(-3.301 40.594)
716.1025 | 697 | POINT(-3.273 40.615) | POINT(-3.268 40.61)
655.39514 | 862 | POINT(-3.226 40.621) | POINT(-3.234 40.626)
659.81757 | 501 | POINT(-3.207 40.642) | POINT(-3.201 40.642)
654.524 | 943 | POINT(-3.164 40.666) | POINT(-3.168 40.658)
To summarize - my recommended approach to calculating elevation profiles and flightlines is:
- create a spatial index to make the nearest neighbor searches fast
- query between lines using the geography type so the shortest path is over a sphere not a straight line
- use the index ordered distance operator to find the shortest distance between two points
- use the nearest neighbor operator with a lateral join to elevation points.